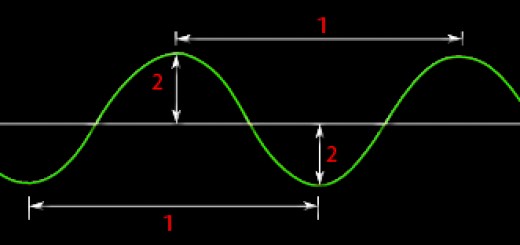
Właściwości dźwięku saksofonu

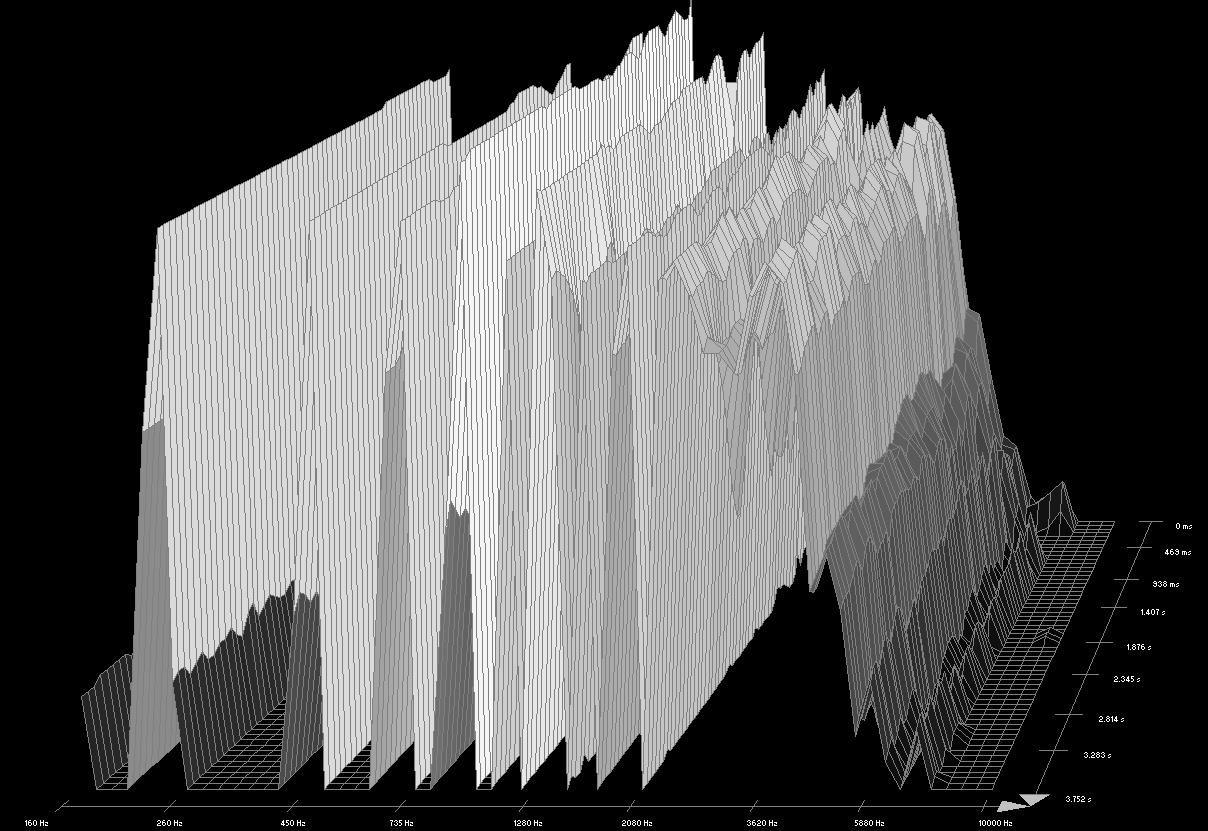
Trochę fizyki związanej z akustyką rury saksofonu.

Oporność akustyczna (podatność akustyczna) – liczba charakteryzująca reakcję gazu lub cieczy na przemieszczającą się w nim falę akustyczną.

W najprostszym przypadku nieskończenie długiej rury o stałym polu przekroju (S) oporność akustyczna
Z = p/(vS)
gdzie:
p – ciśnienie akustyczne,
v – średnia prędkość cząstek wykonujących drgania pod wpływem fali akustycznej.

W ogólnym przypadku (gdy drgania cząstek nie są zgodne w fazie z drganiami fali akustycznej) oporność akustyczna jest wielkością zespoloną, jej składowa urojona nosi nazwę podatności akustycznej.

Opór akustyczny (impedancja akustyczna) – wielkość charakteryzująca reakcję ośrodka sprężystego na zaburzenie wywołane rozchodzącą się w nim falą akustyczną;
jednostka: Pa • s/m3 (1 Pa • s/m3 = 1 rayl).
Opór akustyczny jest wielkością zespoloną a w przypadku fali płaskiej – rzeczywistą.
Obliczony na jednostkę powierzchni jest równy iloczynowi gęstości ośrodka i prędkości rozchodzenia się w nim dźwięku.

Fale akustyczne (fale sprężyste) – zaburzenia mechaniczne ośrodka sprężystego, nie powodujące przesunięcia średnich położeń atomów ośrodka.
W cieczach i gazach fala akustyczna jest falą podłużną, w ciałach stałych może być zarówno falą podłużną, jak i poprzeczną.

W ujęciu bardziej tradycyjnym fale akustyczne to fale odczuwane przez ucho ludzkie jako dźwięk.

Fale akustyczne podlegają prawu odbicia, załamania (refrakcji), dyfrakcji i interferencji.

Ciśnienie akustyczne – zmienne w czasie ciśnienie panujące w ośrodku, wywołane przez zaburzenia o charakterze drgań. Ciśnienie akustyczne opisuje się jako falę rozprzestrzeniającą się lub stojącą i sumuje się je z ciśnieniem statycznym ośrodka (np. atmosferycznym).

Ciśnienie akustyczne odbieramy jako dźwięki. Dźwięki słyszalne dla człowieka to ciśnienia akustyczne mieszczące się w przedziale od 2•10-5 Pa do 2 Pa.

Fala – przenoszące energię zaburzenie pola fizycznego, rozchodzące się ze skończoną prędkością. Jeśli kierunek zaburzenia jest prostopadły do kierunku rozchodzenia się fali – fala jest falą poprzeczną (np. fale elektromagnetyczne);
jeśli oba kierunki są zgodne – fala jest falą podłużną (np. fale ciśnienia akustycznego w powietrzu).

Fala opisywana jest funkcją położenia i czasu u(r,t), spełniającą w ośrodku jednorodnym równanie falowe:
gdzie: Δ – laplasjan, v – stała (prędkość fazowa).

Szczególnymi przypadkami fal są fale monochromatyczne o różnej symetrii: – fala płaska, wtedy u= u0cos(ωt-k•r+δ), gdzie: u0 – amplituda fali, ω = 2π /T – częstość kołowa fali, T – okres, k = (2π /λ)x – wektor falowy, λ- długość fali, x – wersor kierunku rozchodzenia się fali, δ – faza początkowa fali,
– fala kulista (o symetrii sferycznej, rozbiegająca się izotropowo), wtedy: u=(r-1)•f(r-vt), gdzie f jest dowolną funkcją różniczkowalną z drugimi pochodnymi (może to być fala sin lub cos, ale nie tylko), v to prędkość fazowa fali,
– fala cylindryczna (o symetrii cylindrycznej), równanie falowe przekształca się wtedy w równanie Bessela, zmiana amplitudy z promieniem dana jest przez funkcję Bessela rzędu zerowego.

W jednorodnym ośrodku fale rozprzestrzeniają się zgodnie z prawami optyki geometrycznej, w obecności przeszkód pojawiają się odstępstwa od tych praw (dyfrakcja).

Fale nakładające się na siebie mogą podlegać interferencji, dudnieniu lub modulacji.
Dźwięk – fala akustyczna rozchodząca się w ośrodku sprężystym lub wrażenie słuchowe wywołane tą falą. Przyjmuje się, że człowiek słyszy dźwięki o częstościach od 16 Hz do 20 kHz. Drgania o mniejszej częstości to infradźwięki, a o wyższej ultradźwięki. Najłatwiej słyszalne są dźwięki o częstości ok. 1000 Hz.

Fizycznymi aspektami dźwięków są:
– widmo,
– natężenie,
– długość trwania dźwięku,
– zmiany w czasie trwania dźwięku.

Ze względu na rodzaj widma, dźwięki klasyfikuje się następująco:
1) ton (dźwięk prosty) – drganie sinusoidalne o jednej częstości,
2) wieloton harmoniczny (dźwięk złożony) – drganie będące sumą drgań sinusoidalnych o częstościach będących wielokrotnościami (1,2,3,…) częstości podstawowej,
3) wieloton nieharmoniczny – drganie będące sumą nie uporządkowanych drgań,
4) szum – dźwięk o ciągłym widmie.

Drgania (oscylacje) są procesami fizycznymi, które klasyfikuje się na podstawie własności matematycznych opisujących je funkcji, na przemian rosnących i malejących.

Wyróżnia się drgania probabilistyczne (jeśli przyszły stan nie daje się jednoznacznie ściśle określić) i deterministyczne. Drgania deterministyczne dzielą się na okresowe i nieokresowe (periodyczne i nieperiodyczne).

Okresem drgań nazywamy czas potrzebny do wykonania jednego cyklu drgań. Jeśli amplituda maleje w czasie, drgania nazywamy gasnącymi (tłumionymi). Drgania można też dzielić na swobodne i wymuszone (wywołane zewnętrzną, zmienną w czasie, siłą). Drgania deterministyczne opisywane są równaniami różniczkowymi.
Szczególnym rodzajem drgań są drgania harmoniczne, tj. okresowe, o stałej amplitudzie, opisane sinusoidą.
Ze względu na prostotę opisu, drgania harmoniczne są wykorzystywane do opisu wielu drgań rzeczywistych jako ich przybliżenie (lub poprzez rozkład na nie).

Najprostsze równanie opisujące drgania harmoniczne (dla ciężarka zawieszonego na sprężynie) ma postać:
mx” (t) + kx(t) = 0.
Rozwiązaniem jest funkcja
x(t)=Asinωt+ϕ0,
gdzie A – amplituda drgań, ω = 2πν = (k/m)0.5, ω – częstość kołowa (ν – częstość drgań), k – współczynnik sprężystości, m – masa ciała, ϕ0 – faza początkowa.

Ze względu na fizykę procesów wyróżnia się drgania mechaniczne i elektryczne.